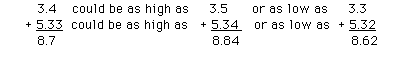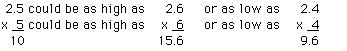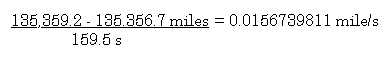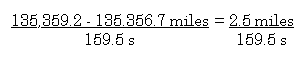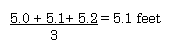Measurement (not really much to say here)

1. Pick the right device.

2. Read the scale

a. digital .....read the scale

b. analog: read the value and then estimate last digit. Generally one can estimate to 10% of the smallest scale increment.

Since the last digit is estimated there is error associated with it. Unless stated otherwise the error is assumed to be ±1 (the smallest increment).

e.g.

3.45 g means 3.45 ± 0.01 g

79.5 g means 79.5 ± 0.1 g

 

Reporting measurements

1. Units: do not forget the units. Additionally, include names when appropriate.

do not simply write 3.19 g, but 3.19 g CuSO₄

2. Significant Figures tell how precisely the measurement was made.

A student uses a 4 decimal place balance to determine the mass of a sample of NaCl. Should the mass be reported as 5 g, or 5.0000 g?

5.0000 g is the correct answer. If one were to write 5 g of NaCl the assumption is that the error is ±1 g when the actual measurement is precise to ±0.0001 g.

Using Significant figures

Two important steps with sigfigs...

1. Determining the number of significant figures in a measurement.

a. All non-zero numbers are significant.

b. Zero's are significant if

i. they are between two non-zero numbers

ii. they occur before and after the decimal point of a number whose absolute value is > 1

e.g. in 10.0 the zeros are significant.

iii. they occur after a non-zero number in a number whose absolute value is < 1.

e.g. in 0.0560 the leading zeros are not significant, but the trailing zero is.

2. Determining the number of significant figures that should remain after performing mathematical manipulations with the numbers.

There are two sets of rules

a. addition/subtraction

the result of adding two numbers together should be precise to the place that corresponds to the least precise measurement

b. multiplication/division

the result of multiplying two numbers should have the same number of significant figures as the number with the fewest significant figures.

examples

a. Addition/subtraction

The measuments 3.4 in and 5.33 in could be as high as 3.5 and 5.34, or as low as 3.3 and 5.32

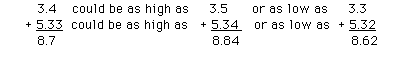
An answer of 8.73 would mean that the sum of the measurements could be 8.74 to 8.72. Obviously, the sum can be outside this small range due to the error associated with the measurement 3.4. To ensure that the result falls within the real window of uncertainty (i.e. 8.84 to 8.62) the result is reported as 8.7 in.

b. Multiplication (Determine the area of a rectangle with side lengths equal to 2.5 and 5 cm)

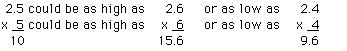
Once again using to many significant figures in the answer would be misleading. The product of 5 and 2.5 is 12.5, but this number implies a range from 12.4 to 12.6 cm². Clearly, the actual area could be outside the range of 12.4 to 12.6 cm². 12.5 can rounded to 13. The result "13" implies from 12 to 14 the actual possibilities are still outside this range. To ensure that the result does not imply more precision than is warranted, the result must be reported as 10 cm², which implies that the number could be anywhere from 0 to 20 cm².

Combining Mathematical operations

Losing Sgnificant Figures (lets demonstrate with an example)

Because you are on a long automobile trip and you are bored, you decide to determine your average velocity in miles per second. The only instruments available are your odometer, and your wrist watch.

You start the timer on your wrist watch when the odemeter reads 135,356.7 miles (did I mention that you are driving an old car?) and you stop the timer when the odometer reads 135,359.2 mile. Your stopwatch indicates that 159.5 seconds have elapsed.

Average speed equals distance traveled divided by elapsed time.

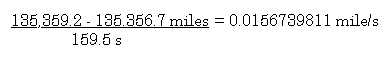
So, how many significant figures should be used in your answer?

2

Why?

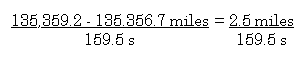
The difference is 2.5 and this number is the number that limits the number of significant figures the answer can contain.....so

0.016 mile/s (Incidentally, you are travelling 56 mph.)

Exact Numbers

Some numbers have an unlimited number of significant figures. These numbers are called exact numbers. These numbers are numbers about which one is absolutely certain.

•Exact numbers never limit the number of significant figures.

•Exact numbers have as many significant figures as the problem requires.

•Exact numbers are numbers that are defined to be a certain value.

For example

12 inches = 1 foot

5280 feet = 1 mile

2.54 cm = 1 inch

1 km = 1000 m

•Exact numbers are things that can be counted. (This statement must be applied cautiously. Every several years the United States attempts to count the number of people in the country. Clearly the population determined by the Census Bureau is not an exact number.)

An Example

Three measurements were made of the length of my office.

5.0 feet, 5.1 feet, and 5.2 feet. Determine the average length.

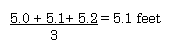
5.1 feet is correct. The "3" is an exact number so it does not limit the number of significant figures contained in the result.

An alternate view point... the answer should have three significant figures.

Since 5.0 + 5.1 + 5.2 = 15.3 and 15.3 (following the sigfig rules for addition produces a number with three sig-figs) has three significant figures, the answer should also have three significant figures. (return to conversions page)

back to GenChem Homepage