![]()
Balancing Red-Ox equations
some redox reactions can be balanced by simple trial and error
![]()
The interesting thing to note is
Every time an Ag+ is reduced to Ag 1 e- is
required.
Every time a copper atom is converted to a Cu2+ ion 2 e-'s
are released.
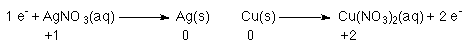
So, everytime 1 Cu atom is oxidized 2 e-'s are released; these two e-'s are used to reduce Ag+ to Ag. However, the Ag reaction comsumes 1 e-, and the Cu reaction releases 2 e-'s. Since we cannot have electrons just floating around every time 1 Cu is oxidized 2 Ag+'s are reduced.
Notice that you can use the number of electrons to balance the two half reactions.
Let's use this technique to balance more difficult reactions.
1. Separate into half reactions;
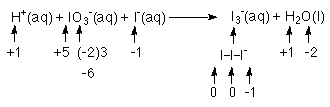
This problem is a tough one because you must realize that
I3- is both the oxidation product and the
reduction product!
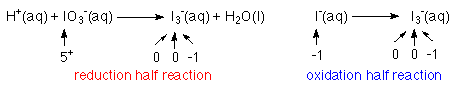
The reactions are called half reactions, because each is only half of the whole reaction.
2. Balance the elements that are being oxidized and reduced.
![]()
3. Determine the number of electrons that are being moved in each half reaction.
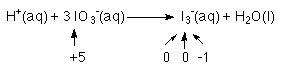 |
|
2 of the 3 I's go from an oxidation # of +5 to 0
to each I 5 e-'s must be added for a subtotal of 10 e-1 of the 3 I's goes from +5 to -1
6 e-'s must be added to go from +5 to -116 e-'s must be added to the reactants of this half reaction.
|
|
|
Now, the other half reaction...
|
|
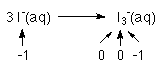 |
2 of the 3 I's go from an oxidation # of -1 to 0
from each I 1 e-'s must be removed for a subtotal of 2 e-1 of the 3 I's does not change
1 I- remains as an I-2 e-'s must be removed from the reactants, but since we don't subtract things n chemistry, we say that 2 e-'s must be produced by this half reaction.
|
|
|
4. Determine least common multiple relationship and multiply
That is, if one half reaction needs 16 e-'s and the other reaction produces 2 e-'s.The oxidation reaction must occur 8 times to produce 16 e-'s.
This is important. This is how we relate the oxidation half reaction to the reduction half reaction.
5. Add the half reactions back together.
6. Balance the O's in the reaction by adding water.
Above there are 9 O's on the reactant side, and 1 O on the product side.
So, 8 H2O's must be added to the product side.
7. Balance H's using H+.
![]()
check your answer....
All the numbers in the equation above are divisible by 3!
![]()
The quickest way to check your answer is to check the charges. If the charges do not balance then you have done something wrong. If the charges balance you are probably OK.
Another Example
The following reaction occurs in aqueous base.
Since the reaction occurs in aqueous base
water and hydroxide are present.
We will add them in later
1. Separate into half reactions;
first determine which atoms are oxidized and which are reduced.
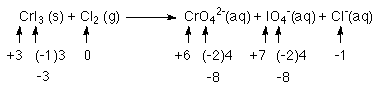
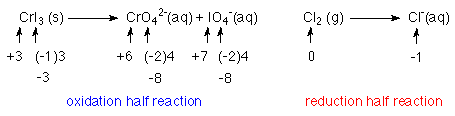
2. Balance the elements that are being oxidized and reduced.
Do not worry about the O's and H's; we will deal with them later.
3. Determine the number of electrons that are being moved.
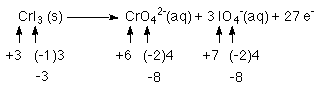
1 Cr atom goes from +3 to +6 releasing 3e-'s
3 I atoms go from -1 to +7 releasing 8 e-'s each
for a total of 3(8) + 3 = 27 e-'s
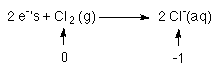
2 Cl atoms each go from 0 to -1
so each Cl needs an e-
for a total of 2 e-'s
4. Determine least common multiple relationship and multiply
That is, if one half reaction needs 2 e-'s and the other reaction produces 27 e-'s.The oxidation reaction must occur 2 times to produce 54 e-'s while the reduction reaction must occur 27 time to consume 54 e-'s.
This is important. This is how we relate the oxidation half reaction to the reduction half reaction.
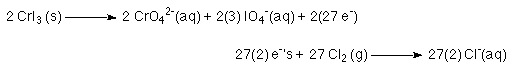
5. Add the half reactions back together.
6. Balance the O's in the reaction by adding water.
Above there are no O's on the reactant side, and 32 O's on the product side.
So, 32 H2O's must be added to the product side.
7. Balance H's using H+.
There are 64 H's on the reactant side, and no H's on the product side.
So, 64 H's need to be added to product side.
![]()
We could have balanced the O's and the H's using OH- and H2O; using H2O and H+ was a trick to make things a bit easier.
8. To eliminate the H+'s add OH- to both sides of the reaction.
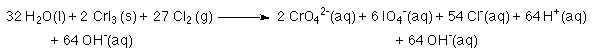
9. The H+ and the OH- combine to form H2O.
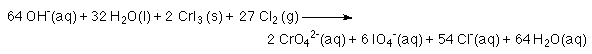
10. Water should not be listed as both a reactant and a product. Cancel water so that it is present as only a reactant or a product.
![]()