|
|
(1) |
Z = # of protons, e = charge of an electron, r = radius)
Bohr created the first model that accounted for the emission of specific frequencies of light from an excited hydrogen atom.
The Bohr model is derived using three statements.
(1) The energy of the electron in a hydrogen atom is the sum of the KE and the PE. The magnitude of the kinetic energy is determined by the movement of the electron. The potential energy results from the attraction between the electron and the proton.
|
|
(1) |
Z = # of protons, e = charge of an electron, r = radius)
(2) The force that keeps the electron in its orbitis generated by the attraction of the electron for the nucleus.
So,
|
|
(2) |
(3) Since experimentation reveals that the energy of an electron in a hydrogen atom must be quantized, Bohr postulated that the angular momentum (mvr) of the electron must be quantized.
|
|
(3) |
So, rearranging equation (3) gives
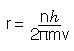
Substituting for r in equation (2) and solving for v gives
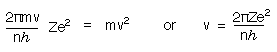
Substituting for v and r in equation (1) gives
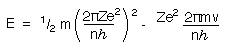
Substituting for v again gives
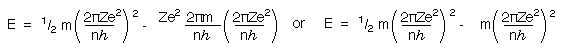
This simplifies to
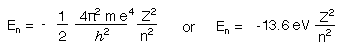
The Bohr equation is in agreement with the Rhydberg equation, which is written below.
RH is the Rydberg constant, 2.18 x 10-18 J.
=
0.
What is the energy and wavelength of the photon released when an electron moves from quantum level 3 to quantum level 2?
E
= (-2.18 x 10-18)
(1/22
- 1/32
)
E
= (-2.18 x 10-18) (0.139)
E
= -3.03 x 10-19 JThe energy that is released is released as a photon. From the photon's point of view the photon is gaining energy (the photon is being created).
Ephoton = h(c/l)
3.03 x 10-19 J = (6.626 x 10-34 J s)(2.9979 x 108 m s-1)/l
l = 6.56 x 10-7 m
l = 656 nm (red)
Although the Bohr atom correctly accounts for hydrogen line spectrum, the model can not be extended to other atoms. Treating an electron as a particle fails to produce a model which can describe all the elements.
